Numeracy, defined as a basic understanding and ability to work with numbers,  matters.

The less numerate earn less and have less wealth.  They’re also more likely to have chronic disease, take more prescription drugs and be less able to follow the (partly numerated) instructions, thus adding more health risk.  Some of this is conflated with other factors but some of it is independently attributed to one’s numeracy.

We’re an industry built on numbers.  Budgets, response rates, cost to raise a dollar, lifetime value calculations…not to mention a need for  slightly more advanced statistical power analysis or significance testing or modeling or, dare I say it, AI.

If low numeracy impacts individual wealth and health it seems plausible it’s also an invisible, negative force in our direct response world.  We don’t know what we don’t know and as it turns out, we often don’t know what we think we know.

Humans are particularly inept with probabilities.  We routinely assign too much risk to low probability events and vice versa.  We use  what’s available and familiar as insight on the likelihood of an event happening, which creates lots of bias.

But hey, “I think I’m above average on numeracy.”  Most people probably do.  The Lake Wobegon effect is real.

Today’s  Puzzler

Here’s a logic and probability puzzle.  Yes, you will be graded (but only pass/fail) and I did pass the test but that’s probably only because I think I read about this ages ago and managed to store it in the recesses of my brain.  So, I probably cheated.

If you fail the test you’ll be in very good company with lots of PhDs in math who were strident, obnoxious, rude and even sexist in incorrectly, correcting the columnist, Marilyn vos Savant, writer of the “Ask Marilyn” column in Parade magazine, circa 1990.

Marilyn, as it turns out, held a Guiness book record for the highest recorded IQ at one point.  There is always someone smarter, even if you are PhD in math at MIT; in this case a newspaper columnist.

The test is famous, it’s called the Monty Hall problem of Let’s Make a Deal fame.

Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say #1, and the host, who knows what’s behind the doors, opens another door, say #3, which has a goat. He says to you, “Do you want to pick door #2?” Is it to your advantage to switch your choice of doors?

Marilyn said “yes”.  It is to your advantage to switch doors.  Here is but one reader’s comment but it is typifies the flurry of borderline hate mail she got.

You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I’ll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don’t need the world’s highest IQ propagating more. Shame!
Scott Smith, Ph.D.
University of Florida

Here is Marilyn’s response back, circa 1990 remember, to her less than polite readers.

Gasp! If this controversy continues, even the postman won’t be able to fit into the mailroom. I’m receiving thousands of letters, nearly all insisting that I’m wrong, including the Deputy Director of the Center for Defense Information and a Research Mathematical Statistician from the National Institutes of Health! Of the letters from the general public, 92% are against my answer, and of the letters from universities, 65% are against my answer. Overall, nine out of ten readers completely disagree with my reply.

So let’s look at it again, remembering that the original answer defines certain conditions, the most significant of which is that the host always opens a losing door on purpose. (There’s no way he can always open a losing door by chance!) Anything else is a different question.

The original answer is still correct, and the key to it lies in the question, “Should you switch?” Suppose we pause at that point, and a UFO settles down onto the stage. A little green woman emerges, and the host asks her to point to one of the two unopened doors. The chances that she’ll randomly choose the one with the prize are 1/2, all right. But that’s because she lacks the advantage the original contestant had—the help of the host. (Try to forget any particular television show.)

When you first choose door #1 from three, there’s a 1/3 chance that the prize is behind that one and a 2/3 chance that it’s behind one of the others. But then the host steps in and gives you a clue. If the prize is behind #2, the host shows you #3, and if the prize is behind #3, the host shows you #2. So when you switch, you win if the prize is behind #2 or #3. You win either way! But if you don’t switch, you win only if the prize is behind door #1.

Still hard to follow and accept, right?  Here’s another way to think about it.  The probabilities don’t change.  That’s the rub.  It doesn’t ever go to 50/50 on the two remaining doors.  The two doors you didn’t pick always had a combined, 66% chance of winning.  When the host took one of those two doors away the 66% still holds except it only applies to one door now.   Here is a visual of the possible outcomes (courtesy of the Wall Street Journal).

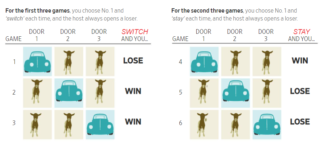
Hopefully that was challenging and got the brain juices flowing for the day if nothing else.  The takeaway,

1. Numeracy matters
2. We can all use more of it
3. There is always someone smarter
4. The professional background is a decent proxy in deciding who, in a given situation, is “smarter”.  It’s true most PhDs were wrong but as Marilyn noted, only at a 65% clip compared to over 90% wrong for the general public.
5. Our gut instinct is powerful.  It’s the force at play right now that has you still not sure you buy the Marilyn answer.

Kevin